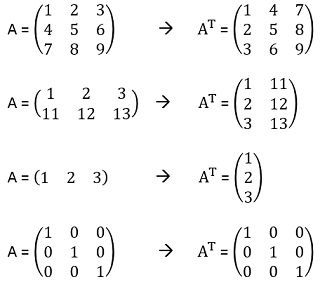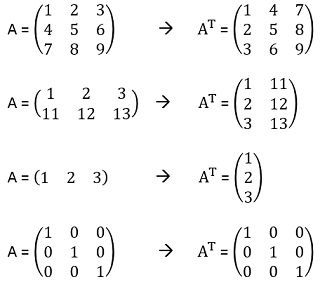Matriz transpuesta

Sea ${\displaystyle A}$ una matriz con ${\displaystyle m}$ filas y ${\displaystyle n}$ columnas. La matriz traspuesta, denotada con ${\displaystyle A^{t}}$.^[1]​^[2]​

Está dada por:

${\displaystyle (A^{t})_{ij}=A_{ji},\ 1\leq i\leq n,\ 1\leq j\leq m}$^[3]​

En donde el elemento ${\displaystyle a_{ji}}$ de la matriz original ${\displaystyle A}$ se convertirá en el elemento ${\displaystyle a_{ij}}$ de la matriz traspuesta ${\displaystyle A^{t}}$.

Ejemplos

${\displaystyle {\begin{bmatrix}a&b\\c&d\\e&f\\\end{bmatrix}}^{t}={\begin{bmatrix}a&c&e\\b&d&f\\\end{bmatrix}}}$

${\displaystyle {\begin{bmatrix}1&2\\3&4\\5&6\\\end{bmatrix}}^{t}={\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}}$

Otro ejemplo un poco más grande es el siguiente:

${\displaystyle {\begin{bmatrix}0&0&4\\1&0&4\\0&1&0\\0&3&2\\0&2&3\\0&3&4\\3&3&1\end{bmatrix}}^{t}\quad =\quad {\begin{bmatrix}0&1&0&0&0&0&3\\0&0&1&3&2&3&3\\4&4&0&2&3&4&1\end{bmatrix}}}$

Propiedades

Involutiva

• Para toda matriz ${\displaystyle A}$,

${\displaystyle (A^{t})^{t}=A\,}$

Distributiva

• Sean A y B matrices con elementos en un anillo ${\displaystyle {\mathcal {A}}}$ y sea ${\displaystyle c\in {\mathcal {A}}}$:

${\displaystyle (A B)^{t}=A^{t} B^{t}\,}$

Lineal

${\displaystyle (c\,A)^{t}=c\,A^{t}}$

• Para el producto usual de las matrices ${\displaystyle A}$ y ${\displaystyle B}$,

${\displaystyle (AB)^{t}=B^{t}A^{t}\,}$

• Si ${\displaystyle A}$ es una matriz cuadrada cuyas entradas son números reales, entonces

${\displaystyle A^{t}A\,}$

es semidefinida positiva.

Definiciones asociadas

Una matriz cuadrada ${\displaystyle A}$ es simétrica si coincide con su traspuesta:

${\displaystyle A^{t}=A\,}$

Una matriz cuadrada ${\displaystyle A}$ es antisimétrica si su traspuesta coincide con su inverso aditivo.

${\displaystyle A^{t}=-A\,}$

Si los elementos de la matriz ${\displaystyle A}$ son números complejos y su traspuesta coincide con su conjugada, se dice que la matriz es hermítica.

${\displaystyle A^{t}={\bar {A}},\quad A=({\bar {A}})^{t}=A^{\dagger }}$

y antihermítica si

${\displaystyle A^{t}=-{\bar {A}}}$

Vale la pena observar que si una matriz es hermítica (matriz simétrica en el caso de matriz real) entonces es diagonalizable y sus autovalores son reales. (El recíproco es falso).

Véase también

• La definición de matriz traspuesta se usa en la definición de Matriz ortogonal.
• Escítala : Instrumento antiguo para cifrar mensajes basado en la trasposición de matrices.
• Trasposición de un operador lineal

Referencias

Enlaces externos

• Hazewinkel, Michiel, ed. (2001), «Transposed_matrix&oldid=15848», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .